Resolução de Sistemas

A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações. Estudaremos a seguir alguns métodos:

Método de substituição

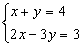
Solução:

• determinamos o valor de x na 1ª equação.
  x = 4 - y

• Substituímos esse valor na 2ª equação.
  2 . (4 - y) -3y = 3 

• Resolvemos a equação formada.

8 - 2y -3y = 3 -5y = -5   => Multiplicamos por -1 5y = 5 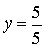y = 1

• Substituímos o valor encontrado de y, em qualquer das equações, determinando x.

x  + y =  4 x  + 1 =  4 x =  4 - 1 x = 3

• A solução do sistema é o par ordenado (3, 1).
  V = {(3, 1)}

Método da adição

Sendo U = , observe a solução do sistema a seguir, pelo método da adição.

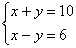
Solução:

• Adicionamos membro a membro as equações:

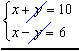
  2x = 16

  

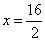
  x = 8

• Substituímos o valor encontrado de x, em qualquer das equações, determinando y: 
  x + y = 10 
  8 + y = 10 
  y = 10 - 8
  y = 2

A solução do sistema é o par ordenado (8, 2).

V = {(8, 2)}

Próximo conteúdo: Inequações do 1º grau